Multi-Agent Path Finding
The Multi-Agent Pathfinding Problem
Multi-Agent Pathfinding (MAPF) is the problem of planning paths for multiple agents without colliding.
Applications
Currently, search-based MAPF solvers perform better than Multi-agent Reinforcement Learning applied to the MAPF problem in restrictive, discrete situations. State-of-the-art MAPF solvers can usually solve up to a low four digit number of agents. The classical application for these kinds of algorithms are logistic warehouses, so for now we might just be contributing ressources for free to Amazon. :/
Assumptions
Common assumptions are:
- the environment is discrete
- an agent executes one action per timestep
- an agent occupies one vertex/node per timestep
Input
The input to a MAPF problem is a triple $<G,s,t>$ consisting of:
-
an undirected graph $G = (V,E)$
-
a mapping $s$ to source vertices with $s: [1,\dots,k] \to V$
-
a mapping $t$ to target vertices with $t: [1,\dots,k] \to V$
Solution
The solution of a MAPF problem is a set $\pi$ of single-agent plans without conflicts: $\pi$ = {$\pi_1, \pi_2, \dots, \pi_k$} where $\pi_i$ denotes the single-agent plan for agent $i$. A single-agent plan is an action mapping $\pi$ (careful: notation overload!) that results in the agent being their target state. We can write this constraint as $\pi_i[|\pi|] = t(i)$.
Note, that $\pi$ does not include the starting position $s(i)$. Instead, the first entry in $\pi$ is the action that performed on the first timestep.
We can also ask, where an agent $i$ is positioned after timestep $x$ (equivalent to asking which node an agent occupies). We would write this as $\pi_i[x]$.
Conflicts
To properly define a MAPF problem, you should cover which of the following conflicts are allowed and which can not appear in a solution $\pi$.
Conflict types:

a) Vertex conflict b) Swapping conflict c) Following conflict d) Circle conflict
Objectives and Constraints
The two most used objective functions are the Makespan and Sum of costs.
Makespan
The Makespan of a MAPF solution is definded as the number of timesteps it takes until all agents reach their goals: $J(\pi) = \max_{1 \leq i \leq k}|\pi_i|$
Sum of costs
The sum of costs objective function takes the length of all individual agent plans into consideration by summing over all action plan lengths: $J(\pi) = \sum_{1 \leq i \leq k}|\pi_i|$
There is also the not so common sum of fuel objective function that counts all non-waiting moves.
An optimal solution to our problem is one that minimizes the chosen objective function $J(\pi)$ (and satisfies all other given constraints).
Constraints
Typical hard constraints that are additionally added are k-robustness (an agent can only move to a vertex that hasn’t been visited by any agent for $k$ timesteps) and formation rules. The k-robustness adresses the possiblity of delays that could result in agents colliding at execution. The goal is to be within a probabilistic margin for conflicts or have a policy that can deal with delays at execution time to prevent conflicts. Formation rules enforce a specific formation of agents, e.g. to allow communication chains via neighboring agents.
Target behaviors
If an agent that already arrived at its target position doesn’t plan on moving away from the target while waiting for other agents to reach their goals it is common to not count the waiting moves towards the sum of cost.
There are two possibilities of handling agents that reach their target. The agent can either stay at the target or disappear at the target. The stay at target behavior is more commonly used because it doesn’t assume that the environment has a special mechanism for handling the transportation of the agent (e.g. to a fixed starting position) upon arriving at the target.
Special MAPF problems
Weighted Actions
MAPF with weighted actions addresses problems, where the assumption of one action per timestep is not useful. The length of an action can be encoded as the weights in an weighted graph, which can be represented as $2^k$-grids or in a generalized form as euclidian (2d) space. Note, that diagonal moves in euclidian space are possible and have an execution (time-) cost of $\sqrt{2}$.
Motion-planning
This takes the MAPF problem to a state-based problem, where the state encodes information like position, orientation and velocity. AN edge between two state configurations can be seen as planning movement (or kinematic motion). If kinematic constraints are added to the MAPF problem, the graph becomes directed.
A (not comprehensive) list of other extensions of MAPF includes
- MAPF with large agents
- MAPF with kinematic constraints
- Anonymous MAPF
- Colored MAPF
- Online-MAPF.
Aspirilo
Aspirilo is a simulator (and visualizer) that includes support for movement-only warehouse setting, which correspond to the multi-agent path finding problem.
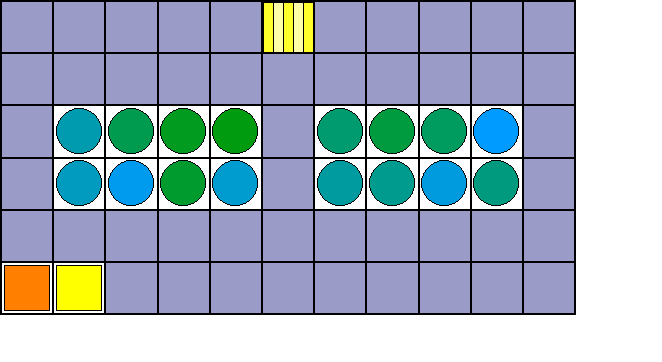
Visualizer Installation
Install the visualizer via:
conda install asprilo-visualizer -c potassco -c potassco/label/dev.
Then you can simply run it using viz:
viz -t <instance.lp>
Or save a plan as a file using these steps:
- Solve the reified test_instance.lp with our meta-telingo
- Only capture the
occurs-atoms using the regular expressionoccurs\(.*\) - Pipe the
occurs-atoms in atest_plan.lpfile using theteecommand that pipes them into the file and prints the atoms - Run the viz using the
test_instance.lpandtest_plan.lpfiles
This command will first use grep to search for all occurrences of the regular expression for the occurs atom in the file “input_file.txt” as before. The output of grep command is piped into sed command which replaces the blank space after each occurs atom with a period. The output of the sed command is then piped into yet another command - tee - which writes the output to both the terminal and the specified file “test_plan.lp”. Then we use echo to add a last period after the last occurs atom because it didn’t have a blank space to be replaced after it.
The resulting plan is a valid input for the aspirilo visualizer. We save this plan as test_plan.lp to call the aspirilo visualizer and use it together with the corresponding instance.
clingo encoding.lp test_instance.lp --output=reify | clingo - meta-telingo.lp output-meta-telingo.lp -c horizon=9 | grep -o "occurs\(.*\)" | sed 's/ /\./g' | tee test_plan.lp; echo . >> test_plan.lp
viz -l test_instance.lp test_plan.lp
Introduction
Go to:
/home/till/Desktop/GitHub/telingo-wise22-23-themetaprogrammers/aspirilo-meta-telingo
Great, we got a model! I believe that only the occurs(object(robot,1),action(move,(1,0)),2) atoms are part of the solution. This example atom says that robot1 moved 1 cell up in timestep 2. The rest of the atoms are all part of the initialization of the instance.
Now we can try to break everything by converting it to meta-telingo :D
To solve an instance with our meta-telingo.lp program, you need to first reify encoding.lp (which includes action-M.lp, a goal-test goal-M.lp and an output conversion file output-M.lp) and the instance, in our case test_instance.lp. We also automatically include input.lp in the action-M.lp file. Then you pipe the reified facts into meta-telingo.lp to solve it using clingo, in this case using horizon=15 and showing the first model by setting the number of models parameter to 1.
clingo encoding.lp test_instance.lp --output=reify | clingo - meta-telingo.lp -c horizon=15 1
For the KRR project, we will restrict ourselves to the movement only (M) domain.
Action-M.lp encoding
- rewrite with
prev()operators instead ofT-1 - add
#externalcommands with all atoms that are possible for this atom included on the right hand side to avoid unsafe atmoms, e.g.#external move(R,C) :- robot(R), vertex(C)(maybe instead of:-only write:, try both and test which one works. Also look in the files from the beginning of the semester to see how we did it there.)
Include the input encoding
For the input.lp encoding, we’ll have to change the path since it’s in the same directory:
#include "./input.lp".
Position/3
The robot R is at cell C, which is a tuple with the coordinates (X,Y), at time step T.
position(R,C,T) :- move(R,D,T), position(R,C',T-1), nextto(C',D,C).
:- move(R,D,T), position(R,C ,T-1), not nextto(C ,D,_).
We’ll now modify all of the code in action.lp to use prev(atom(T)) instead of atom(T-1).
For the previous code block, this is the result:
position(R,C,T) :- move(R,D,T), prev(position(R,C',T)), nextto(C',D,C).
:- move(R,D,T), prev(position(R,C ,T)), not nextto(C ,D,_).
Externals
Now that we have included some meta-telingo prev operators, we’ll have to tell clingo to not delete them in preprocessing by using #external.
%*
externals
*%
aux_cell(C) :- nextto(C,_,_).
aux_cell(C) :- position(_,C,_).
#external prev(position(R,C,T)) : robot(R), aux_cell(C), time(T).
#external initially.
#external finally.
#external horizon.
Here is the program with all the discussed changes so far:
#include "./input.lp".
#const horizon=15.
time(1..horizon).
direction((X,Y)) :- X=-1..1, Y=-1..1, |X+Y|=1.
nextto((X,Y),(X',Y'),(X+X',Y+Y')) :- position((X,Y)), direction((X',Y')), position((X+X',Y+Y')).
{ move(R,D,T) : direction(D) } 1 :- isRobot(R), time(T).
% - move/3 ----------------------------------------------------------------------
position(R,C,T) :- move(R,D,T), prev(position(R,C',T)), nextto(C',D,C).
:- move(R,D,T), prev(position(R,C ,T)), not nextto(C ,D,_).
% - inertia ---------------------------------------------------------------------
position(R,C,T) :- prev(position(R,C,T)), not move(R,_,T), isRobot(R), time(T).
% - edge collision --------------------------------------------------------------
moveto(C',C,T) :- nextto(C',D,C), prev(position(R,C',T)), move(R,D,T).
:- moveto(C',C,T), moveto(C,C',T), C < C'.
% - vertex collision ------------------------------------------------------------
:- { position(R,C,T) : isRobot(R) } > 1, position(C), time(T).
% - auxiliaries -----------------------------------------------------------------
:- { position(R,C,T) } != 1, isRobot(R), time(T). % REDUNDANT but PERFORMANT?
%*
externals
*%
aux_cell(C) :- nextto(C,_,_).
aux_cell(C) :- position(_,C,_).
#external prev(position(R,C,T)) : robot(R), aux_cell(C), time(T).
#external initially.
#external finally.
Let’s try to run it.
clingo encoding.lp test_instance.lp --output=reify | clingo - meta-telingo.lp -c horizon=15 1
Reading from - ...
Solving...
UNSATISFIABLE
Models : 0
Calls : 1
Time : 11.617s (Solving: 0.00s 1st Model: 0.00s Unsat: 0.00s)
CPU Time : 11.616s
This should have been satisfiable, so we are not finished yet. Let’s try to remove the timestep atoms.
Time
Now comes the hardest step: We will have to remove all timesteps T from the code since the time is already being handled in meta-telingo.lp.
The goal-M.lp file before removing the timesteps:
processed(A,R) :- ordered(O,A), shelved(S,A), isRobot(R), position(S,C,0),
position(R,C,horizon).
processed(A) :- processed(A,R).
:- ordered(O,A), not processed(A).
The output-M.lp file before removing the timesteps:
#show.
#show init/2.
#show occurs(object(robot,R), action(move,D), T) : move(robot(R),D,T).
The old input.lp file before removing timesteps:
% --------------------------------------------------------------------------------
% REPRESENTATION
robot(R) :- init(object(robot,R), _).
shelf(S) :- init(object(shelf,S), _).
station(P) :- init(object(pickingStation,P), _).
product(A) :- init(object(product,A), _).
isRobot(robot(R)) :- robot(R).
isShelf(shelf(S)) :- shelf(S).
isStation(station(T)) :- station(T).
isProduct(product(A)) :- product(A).
isOrder(order(O)) :- order(O).
order( O ) :- init(object(order,O), _).
ordered(order(O),product(A)) :- init(object(order,O), value(line,(A,_))). % IGNORING QUANTITIES
target(order(O),station(P)) :- init(object(order,O), value(pickingStation,P)).
shelved(shelf(S),product(A)) :- init(object(product,A), value(on,(S,_))). % IGNORING QUANTITIES
position( (X,Y)) :- init(object(node,_), value(at,(X,Y))).
position(station(P),(X,Y)) :- init(object(pickingStation,P), value(at,(X,Y))).
position( robot(R),(X,Y),0) :- init(object(robot,R), value(at,(X,Y))).
position( shelf(S),(X,Y),0) :- init(object(shelf,S), value(at,(X,Y))).
highway( C ) :- init(object(highway,_), value(at,C)).
References
- Stern, R., Sturtevant, N., Felner, A., Koenig, S., Ma, H., Walker, T., … & Boyarski, E. (2019). Multi-agent pathfinding: Definitions, variants, and benchmarks. In AAAI/ACM Conference on AI, Mobility, and Autonomous Systems (pp. 75-82). (arXiv)
- Kaduri, Omri: From A* to MARL (5 part blogpost series)
- Aspirilo (warehouse simulator) website.
- Thumbnail taken from here.