Intro

If we want to use n-step TD-rollouts, there are some caveats that should be considered - we’ll adress them in this post.

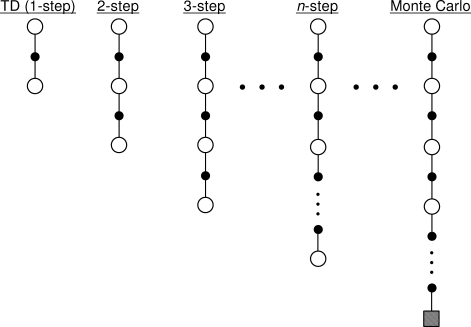
Example: 3-step update

s₁ s₀ s₂ s₃ a₀~π(s₀) a₁~π(s₁) a₂~π(s₂) r₁ r₂ r₃

The TD-Error based on 3 timesteps, in which we collected the rewards $r_1, r_2, r_3$, becomes:

\[\delta_3 Q(s_0, a_0) = r_1 + \gamma r_2 + \gamma^2 r_3 + \gamma^3 arg\max_{a'} Q^{\pi}(s_3, a')\]

Problem

  • longer TD-rollouts have a high variance (because the space of n-step rollouts is larger than the space of 1-step rollouts) $\rightarrow$ we should attribute a lower weight to future errors
  • we are using exponential decay because the number of possible rollouts grows exponentially (with the exponent being the number of follow-states = branching-factor)

Solution: Weighted average $\delta(\lambda)$ with hyperparam. $\lambda \in [0,1]$

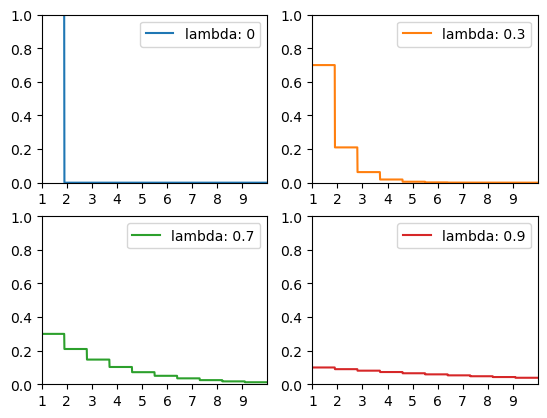
Exponentially weighted average of TD-Errors:

\[\delta(\lambda) = (1 - \lambda) \sum_{k=0}^{\infty} \lambda^{k} \delta_{k+1} Q(s,a)\]
  • weighted towards nearer-term TD-Errors
  • if we set the $\lambda = 0$, we get the usual TD(1-step) Error

To examine the weighting, here are a couple of examples:

Temporal-Difference learning algorithm = TD($\lambda$):

Input: An MDP. Output: A policy $\pi \approx \pi^{*}$

  1. While not converged:
    1. Sample an episode with n steps using the policy $\pi$
    2. $\delta(\lambda) \leftarrow \sum_{k=1}^{n} (1 - \lambda) \lambda^{k-1} \delta_k Q(s,a)$ // get the weighted average
    3. $Q^{\pi}(s,a) \leftarrow (1 - \alpha)Q^{\pi}(s,a) + \alpha \delta(\lambda)$
    4. Improve $\pi$ by increasing $\pi(arg\max_a Q^{\pi}(s,a) | s)$
  2. Return policy $\pi$ with $\pi(s) = arg\max_a Q^{\pi}(s,a)$ for all $s \in S$.

TD($\lambda$) vs TD(0)

By capturing long-term dependencies, TD($\lambda$) should bootstrap more quickly compared to TD(0).

References

  1. Thumbnail from Mark Lee 2005-01-04.
  2. Sutton & Barto: Reinforcement Learning

Post a comment.