Monte-Carlo Tree Search
Intro
Monte-Carlo Tree Search (MCTS) is an algorithm you can use to explore a tree of states by sampling random episodes with a guidance policy that can be thought of like an heuristic. When we sample a lot of episodes, many of them will have the same beginning (because the number of possiblilities grows exponentially in the number of timesteps, depending on the state branching factor) and theirfore the beginning of episodes is probably shared by multiple episodes.
You can think of Monte-Carlo Tree Search as generating the state-tree with guidance of a policy $\pi^s$, similar to heuristic-driven search like $A^{*}$.
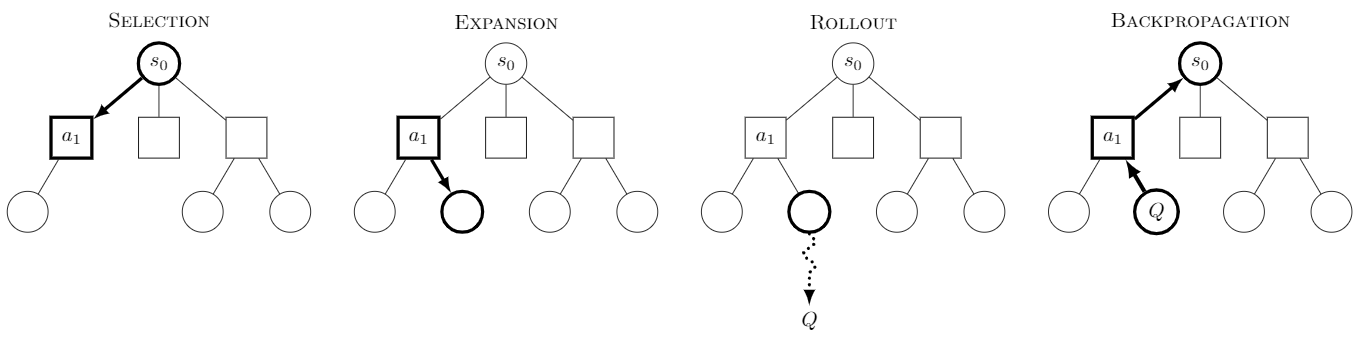
Monte-Carlo Tree Search Algorithm:
- Node selection:
- use a (stochastic) selection policy $\pi^{s}$ to select nodes until we are at a node with no children
- Expansion:
- expand this node (add one or more children according to the policy $\pi^{s}$)
- Simulation:
- sample one episode according to $\pi$ (could be another policy than $\pi^s$)
- observe the value/reward (could be the reward or outcome of a game, i.e. if you won or lost)
- Backpropagation:
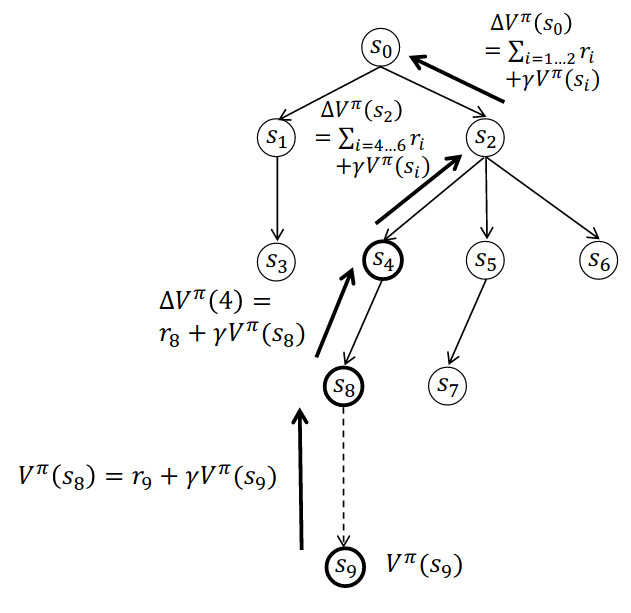
- update $V^{\pi}$ (or $Q^{\pi}$) for all nodes along the trajectory starting from the bottom (= bootstrapping)
- i.e. start with $\Delta V^{\pi}(s_8) = r_9 + \gamma V^{\pi}(s_9)$ for updating the value of state $s_8$
Parallelization
There are three main approaches to parallelization, and the one that sounds most interesting to me (because of simplicity) is number one:
leaf parallelization:- execute multiple playouts (=rollouts) from one leaf node in parallel.
For completeness, the other two approaches are:
root parallelization:- build independent trees in parallel and use all the roots (e.g. mean of all $s’$ one step from the root with $S_t = s_{\text{root}}, S_{t+1} = s’$) to make the final decision
- probably takes too much memory for a small project
tree parallelization:- build one tree in parallel, using mutually exclusive write-access (i.e. a mutex)
- this is hard to implement
References
- Thumbnail from Wikipedia: MCTS_Algorithm
- Tree example from Scheffer, T. Intelligent Data Analysis 2: Reinforcement Learning 2
- Sutton & Barto: Reinforcement Learning
- Parallelization techniques from Wikipedia: Monte Carlo tree search.