COVID-19 Particle-Simulation

Abstract

Wir simulieren den Ausbruch der ursprünglichen COVID-19 (Coronavirus Disease 2019) Pandemie, die durch den SARS-CoV-2 Coronavirus übertragen wird. Dafür kann das Susceptible-Infected-Recovered (SIR) Modell als Differentialgleichungssystem verwendet werden; es ist aber auch eine Partikelsimulation des Susceptible-Exposed-Infected-Recovered (SEIR) Modells möglich, bei der man die Interaktionen einzelner Agenten (Partikel) simuliert [3]. Beide Modellvarianten haben verschiedene Vor- und Nachteile. Differentialgleichungen sind die häufigere Variante in der Praxis [4], da aufgrund der simplen Modellierung des Problems viele Konfigurationen der Parameter simuliert werden können. Zusätzlich ist der Entwicklungsaufwand ist deutlich niedriger verglichen mit dem agentenbasierten Modell. Dafür generiert eine agentenbasierte Simulation umfassendere Daten zur weiteren Analyse, die potentiell mehr Erkenntnisse hervorbringt. Die Anzahl der zu simulierenden Agenten befindet sich für lokale Gebiete (wenige Quadratkilometer Fläche) im umsetzbaren Rahmen. Deswegen fokussieren wir uns auf den Golmer Universitätskampus der Universität Potsdam und implementieren das SEIR-Modell als agentenbasierte Partikelsimulation, um informierte Schlüsse aus den detaillierteren Daten ableiten zu können.

Zielstellung und Umfang

Das Ziel des Projekts ist es, die Ausbreitung des SARS-CoV-2 Coronavirus durch eine Simulation auf dem Golmer Campus der Universität Potsdam zu simulieren und dabei Merkmale der Pandemie zu untersuchen. Wir vergleichen die Eigenschaften und Nützlichkeit von zwei Modellen (SIR und SEIR), die für die Simulation verwendet werden können und präsentieren unsere Implementierung einer Partikelsimulation des SEIR-Modells mit einem integrierten Flow Field Pathfinding Algorithmus. Anschließend zeigen wir die Ergebnisse für ein Beispielexperiment mit unserem Simulator und erklären die Funktionsweise und Benutzung.

Aufbauend auf unserem Projekt könnte man verschiedene Parameter testen und weitere Features implementieren, um beispielsweise informierte Entscheidungen zur Online-Lehre und Maskenpflicht auf dem Campus zu treffen oder die Ausbreitung des Virus in einem größeren Gebiet mittels einer höheren Auflösung zu simulieren. Es gibt viele Möglichkeiten für die Integration von echten Daten, u.a. könnte die Anzahl der Personen pro wissenschaftlichem Fachbereich ermittelt werden und in die Anzahl der Personen und Auswahl der Ziele eingehen (ein Physiker geht mit deutlich höherer Wahrscheinlichkeit zum Physikgebäude als ein Biologe). Weiterhin könnte man den Zug verwenden (der bereits funktionsfähig ist), um Einblicke zu bekommen, wie sich das Pendeln von und zur Universität auf die Pandemieverbreitung auswirkt.

Um den Simulator tatsächlich als Hilfsmittel für Entscheidungen zu verwenden, sollten die generierten Daten vorerst mit echten Daten der letzten beiden Jahre verglichen werden, um den Realitätsgrad und potentielle Abweichungen zu ermitteln. Wir hoffen allerdings, dass das Tool in naher Zukunft nicht mehr gebraucht wird und die Pandemie kontrolliert endet.

Einleitung

Eine neue Art des Coronavirus kann sich in einer Bevölkerung ausbreiten, wenn die Variante des Virus von Tieren (z.B. Fledermäusen) auf Menschen transferierbar ist [1]. Dieser Transfer wird auch zoonotische Übertragung genannt, bei der sich das zoonotische Virus, welches eine organische Struktur ohne Stoffwechsel ist, über Wirtszellen vermehren kann [2]. Die Übertragung des Virus erfolgt durch Tröpfchen und Aerosole (in die Luft verteilte Partikel), die u.a. beim Husten oder Sprechen verteilt werden. Gelangen Partikel mit dem Virus an die Schleimhäute einer gesunden Person, kann sich diese ebenfalls infizieren [5]. Dabei ist die Ansteckungsrate in Gebäuden höher, da sich die Aerosole bei unzureichender Belüftung ansammeln [5]. Dieser Umstand wird in der Partikelsimulation durch die häufigere Kollision von Agenten in Innenräumen indirekt abgedeckt. Deswegen können wir die Ansteckungswahrscheinlichkeit als konstant modellieren, ohne dass die Simulation unrealistisch wird. Wir nehmen in unserem Experiment eine Ansteckungswahrscheinlichkeit von 30% an; diese ist deutlich höher als in der Realität [7], erlaubt uns aber kürzere Simulationen durchzuführen. Die Ansteckungswahrscheinlichkeit kann in der Parameterkonfiguration geändert werden, um verschiedene Szenarien (z.B. das Tragen von Masken) zu simulieren und Strategien für die Pandemieeindämmung abzuleiten.

Wir nehmen an, dass von einer gefixten Populationsgröße $N$ zum Startzeitpunkt ($t=0$) der Pandemie 3 Personen infiziert sind. Bei Durchläufen mit nur einer inifizierten Person wurden manchmal keine anderen Personen rechtzeitig angesteckt, um die anfangs exponentielle Ausbreitung des Virus zu beginnen.

Für die mittlere Inkubationszeit alpha und Kontagiosität beta (Dauer der Ansteckungsfähigkeit) haben wir die Werte alpha=500 Zeitschritte und beta=1000 Zeitschritte angenommen. Die Zeitschritte aus der Simulation können nicht direkt auf eine Zeiteinheit in der Realität übertragen werden, die Abläufe haben aber die gleichen relativen temporalen Verhältnisse. Deswegen ist es wichtig, dass das Verhältnis von Inkubationszeit und Kontagiosität mit echten Daten übereinstimmt. Wir haben als Referenz die Werte $\alpha=5 \text{ Tage}$ und $\beta=10 \text{ Tage}$ vom Robert Koch Institut (November 2021) verwendet [8].

Lösungsstratiegien

Klassisches SEIR-Modell mit Differentialgleichungen

Die Population wird in die folgenden drei Zustände aufgeteilt:

$\text{S = Susceptible}$
$\text{I = Infected}$
$\text{R = Recovered/ Removed}$

Die Änderungsraten für die Anzahl der Partikel pro Zuständ können wir in einem Differentialgleichungssystem für das SRI-Modell wie folgt formulieren [9] [10]:

\[\begin{align*} \frac{dS}{dt} &= - \beta \frac{SI}{N} \\ \frac{dI}{dt} &= \beta \frac{SI}{N} - \gamma I \\ \frac{dR}{dt} &= \gamma I \\ \end{align*}\]

Hierbei wird keine Unterscheidung in die Klassen $\text{Exposed}$ und $\text{Infectious}$ benötigt, da die Unterteilung schon implizit mit den Änderungsraten modelliert wird (wenn mehr Personen infektiös sind, gibt es mehr Statusübergänge von $\text{Susceptible}$ nach $\text{Infected})$.

Die Differentialgleichungen haben einen sehr limitierten Einblick in die simulierte Welt und Population (sie dienen nur als generische Beschreibung der Zustandsänderungen), deswegen werden uns nicht genauer mit dem SRI-Modell in der Form von Differentialgleichungen beschäftigen und gehen zu dem SEIR-Modell als Partikelsimulation über.

SEIR-Modell mit Partikeln

Ein Partikel ist zu jedem Zeitpunkt in genau einem der folgenden Zustände:

$\text{S = Susceptible}$
$\text{E = Exposed (infiziert aber nicht ansteckend)}$
$\text{I = Infectious}$
$\text{R = Recovered/ Removed}$

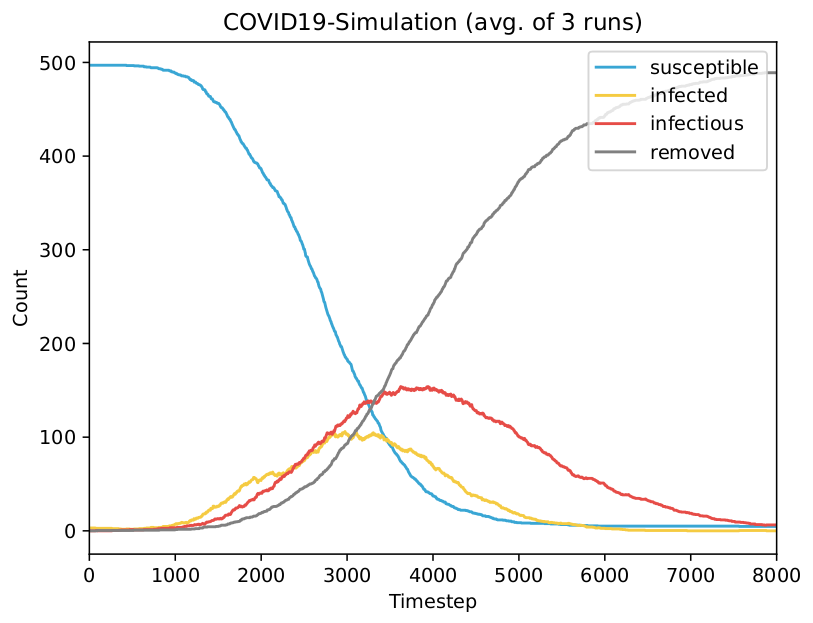
Wir definieren die Mengen $S_t, E_t, I_t, R_t$ als die Mengen der Partikel, die sich zu einem Zeitschritt $t$ im jeweiligen Zustand befinden. Da die Population per Annahme eine feste Größe $N$ hat, gilt für alle Zeitschritte:

\[N = \bar{S_t} + \bar{E_t} + \bar{I_t} + \bar{R_t}\]

Im klassischen SEIR-Modell wird die Anzahl der Zustandswechsel der Partikel mit Raten ausgerechnet [9]. Wir benutzen für unsere Partikelsimulation stattdessen Wahrscheinlichkeiten, die ausdrücken, wie wahrscheinlich es ist, dass ein Partikel in einem Zeitschritt $t$ seinen Zustand wechselt:

$\alpha = \text{Infektionswahrscheinlichkeit}$
$\beta = \text{Inkubationswahrscheinlichkeit}$
$\gamma = \text{Erholungswahrscheinlichkeit}$

Die Wahrscheinlichkeit $\alpha$, dass sich ein Partikel ansteckt, wird bei uns anders als beim konventionellen SIR-Modell gehandhabt. Dort wird der Übergang vom Zustand $\text{S}$ in den Zustand $\text{E}$ als Rate festgelegt; wir definieren hingegen nur die Wahrscheinlichkeit, dass sich ein Partikel ansteckt, wenn es mit einem ansteckenden Partikel kollidiert. Das ist für eine Partikelsimulation notwendig und hat den Vorteil, dass Messungen in der echten Welt über die Ansteckungswahrscheinlichkeit (beispielsweise mit oder ohne Maske) direkt als Parameter in die Simulation eingehen kann, während beim konventionellen SEIR-Modell erst die allgemeine Rate modelliert werden muss, mit der die gesunde Population infiziert wird. Da wir die Partikel als Kreise mit einer Position und einem Radius modellieren, kann man auch den Ansteckungsradius über den Radius der Partikel im Modell anpassen.

Der Status wird für jedes infizierte Partikel (in einem der Zustände $\text{E}$ oder $\text{I}$) einmal pro Zeitschritt zufällig mit den Wahrscheinlichkeiten $\beta$ und $\gamma$ aktualisiert. Ein Partikel im Zustand $\text{Exposed}$ wechselt mit der Inkubationswahrscheinlichkeit $\beta$ in den Zustand $\text{Infectious}$. Vom Zustand $\text{Infectious}$ wechselt es mit der Erholungswahrscheinlichkeit $\gamma$ in den Zustand $\text{Recovered}$, in welchem es dann für den Rest des simulierten Durchlaufs bleibt.

Aufbau der Simulation

Karte

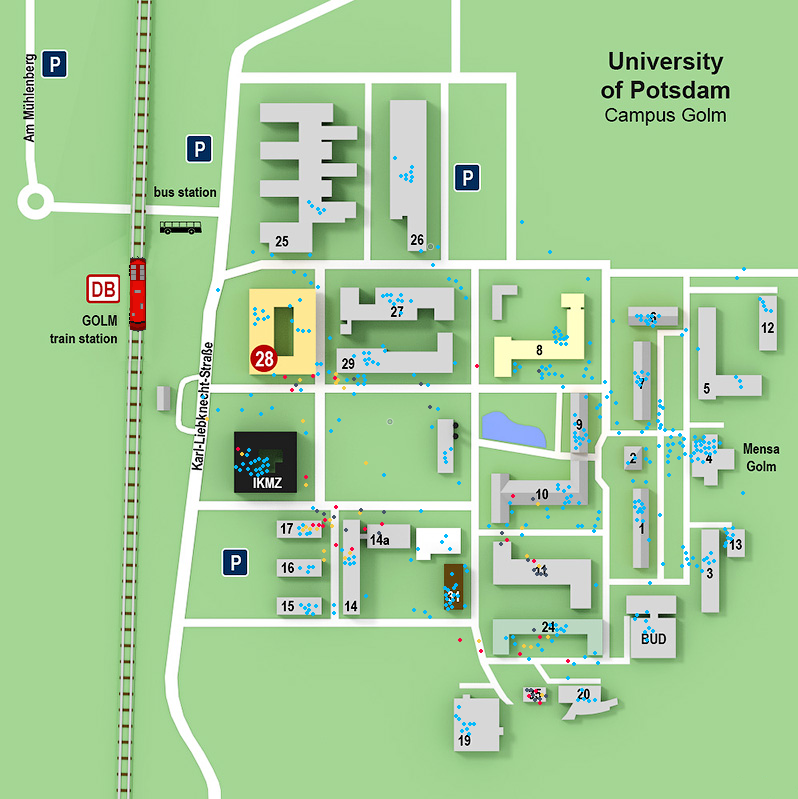
Als Hintergrund der Simulation haben eine Karte von Golm genommen, die von der Webseite der Experimentalphysik stammt [11]. Für jedes Gebäude wurde ein Ursprungspunkt (Origin) festgelegt und Mauern gezogen, die als statische Objekte im PyMunk Simulator verwendet werden. Die Koordinaten der Mauern müssen alle einzeln in Relation zum Ursprungspunkt des Gebäudes gesetzt werden, was ein sehr aufwändiger Prozess war. Um die Koordinaten ablesen zu können, haben wir einen Debug-Modus in den Simulator eingebaut, der alle 10 Zellen einen grauen Punkt und alle 100 Zellen einen roten Punkt zur Orientierung über die Karte legt.

Zug

Der Zug fährt periodisch von oben nach unten auf der Karte und wird dann wieder nach oben zurückgesetzt. Jeder Zyklus dauert 36.000 Pygame-Zeitschritte und wird durch eine Modulo-Rechnung mit dem aktuellen Zeitschritt der Simulation berechnet. Ein Zyklus enthält die folgenden Ereignisse, die relativ zum Beginn des Zyklus angegeben sind: Zu Beginn des Zyklus fährt der Zug mit einer Geschwindigkeit von -1,1 Pixel pro Sekunde in x-Richtung (leicht nach links) und 30 Pixel pro Sekunde in y-Richtung (nach unten). Bei 9.000 Zeitschritten hält der Zug an der Bahnstation an, öffnet die Tür und bleibt stehen. Bei 13.000 Zeitschritten schließt der Zug die Tür und fährt mit der ursprünglichen Geschwindigkeit weiter. Bei 36.000 Zeitschritten kehrt der Zug zum Startpunkt oben auf der Karte zurück und startet den nächsten Zyklus.

Man könnte weiterführend modellieren, dass tatsächlich Personen mit dem Zug fahren; allerdings haben wir für unser Projekt hier eine Grenze für den Entwicklungsaufwand gezogen und dieses Feature nicht implementiert.

Kollisionsbehandlung und probabilistische Infektionsübertragung

In PyMunk werden Kollisionen durch mehrere Funktionen behandelt, wobei die erste der Funktionen “collision_begin” ist. Die anderen Funktionen kümmern sich um die berechnung der neuen Geschwindigkeiten der beiden Körper und Eigenschaftung wie Reibung, Schaden an dem Körper usw. Diese Funktionalitäten sind der Hauptgrund, warum wir die Partikelsimulation nicht von Grund auf geschrieben haben. In der PyMunk Bibliothek werden sehr effiziente Algorithmen verwendet, die durch die Programmiersprace C effizient sind und dadurch auch große Mengen von Partikel handhaben können. Um die Simulation für unser Projekt benutzen zu können, haben wir eine eigene Implementierung der Funktion “collision_begin” geschrieben, um die Infektionsübertragung zwischen Personen zu simulieren.

Die Funktion überprüft zunächst, ob eine der beteiligten Person an der Kollision als infektiös markiert ist (d.h. ihre Dichte ist 0.8). Wir mussten hier die Implementation etwas unüblich “hacken” und die Information über den Status einer Person in der Dichte des Partikels kodieren, da wir sonst nicht mit dem Simulator-Objekt und PyGame kommunizieren können. Falls eine der Personen infektiös ist, wird für jede andere beteiligte Person (deren Dichte 1.0 ist, was für einen gesunden Zustand steht) per Zufall mit der Infektionswahrscheinlichkeit $\alpha$ berechnet ob die gesunde Person infiziert wird oder nicht. Wenn die Person infiziert wird, wird ihre Dichte auf 0.9 gesetzt, um anzuzeigen, dass sie jetzt infiziert ist. Der tatsächliche Status der Infektion (als Attribut des Personen-Objekts) wird dann im nächsten Zeitschritt automatisch über die gegebene Dichte aktualisiert.

In unserer Implementierung wird auch der Ort der Infektionsübertragung gespeichert, indem die Position des infizierten Körpers in eine Liste “collision_points” eingefügt wird. Diese Information kann später verwendet werden, um eine Heatmap aller Übertragungsorte zu erstellen. Dort kann man dann ablesen, welche Orte auf der Karte besonders häufig zu Ansteckungen führen.

Die Klasse “Person” enthält auch die Methode “update_infection_status” die für jede Person in jedem Zeitpunkt aufgerufen wird und die zufällig den Status der Person gemäß dem SEIR-Modell mit den Wahrscheinlichkeiten $\beta$ und $\gamma$ aktualisiert (siehe “SEIR-Modell mit Partikeln”). Dabei werden die durchschnittlichen Zeiten für Inkubation und Ansteckung sowie der aktuelle Zeitpunkt übergeben. Diese Methoden ermöglichen es uns, eine probabilistische Veränderung des Infektionsstatus einer Personen im Laufe der Zeit zu simulieren.

Probabilistische Zielauswahl

Die Agenten besuchen alle Gebäude außer der Mensa und Bibliothek (diese beiden Ziele werden leicht bevorzugt) mit einer gleichverteilten Wahrscheinlichkeit. Die Wahrscheinlichkeit, dass eine Person eines der 30 Gebäude als nächstes Ziel $X$ auswählt, wird wie folgt berechnet:

\[P(X=x_i) = \begin{cases} \frac{1}{10} & \text{if } i \in \{3, 27\} \text{ (Mensa oder Bibliothek)}\\ \frac{1}{35} & \text{sonst.} \end{cases}\]

Die Wahrscheinlichkeit $P$ ist normiert, da

\[2 \times \frac{1}{10} + (30 - 2) \times \frac{1}{35} = 1.\]

Ein Agent verfolgt sein aktuelles Ziel für eine Anzahl von Zeitschritten, die auch normalverteilt bestimmt wird und sich für jedes neue Ziel ändert.

Goal-Based Vector Flow Field Pathfinding

Wir diskretisieren die Karte von Golm in ein $2 \text{D}$-Array mit der Form $800 \times 800$. Jeder Agent kann sich mit kontinuierlichen Koordinaten bewegen seine Position wird für das Pathfinding dann aber auf diskrete Koordinaten abgerundet. Die Zellen des Arrays definiert die Bereiche, in denen Einheiten sich bewegen können. Jede Grid-Zelle kann entweder offen sein, was bedeutet, dass ein Agent diese Zelle durchqueren kann, oder blockiert, was bedeutet, dass die Zelle Teil einer Wand und daher nicht durchquerbar ist.

Partikel bewegen sich durch das Grid folgend einem statischen Flow Field, das nur ein einziges Mal berechnet werden muss und in allen folgenden Simulationen einfach als numpy-file geladen werden kann. Das bedeutet, dass das Pathfinding zur Ausführung der Simulation keine Rechenzeit verbraucht und Agenten direkt den optimalen Weg von ihrer Position zu dem aktuellen Ziel bestimmen können. Man müsste das Flow Field aktualisieren, wenn sich die begehbaren Bereiche des Grids oder der Satz von Zielpunkten ändern - was bei uns nicht mehr der Fall ist, da wir bereits alle Gebäude eingebaut haben. Es gibt noch die Möglichkeit, die Gehwege abzugrenzen, aber unserer Erfahrung nach ist es realistischer, wenn die Studenten auch über den Rasen gehen und alle möglichen Abkürzungen nehmen können.

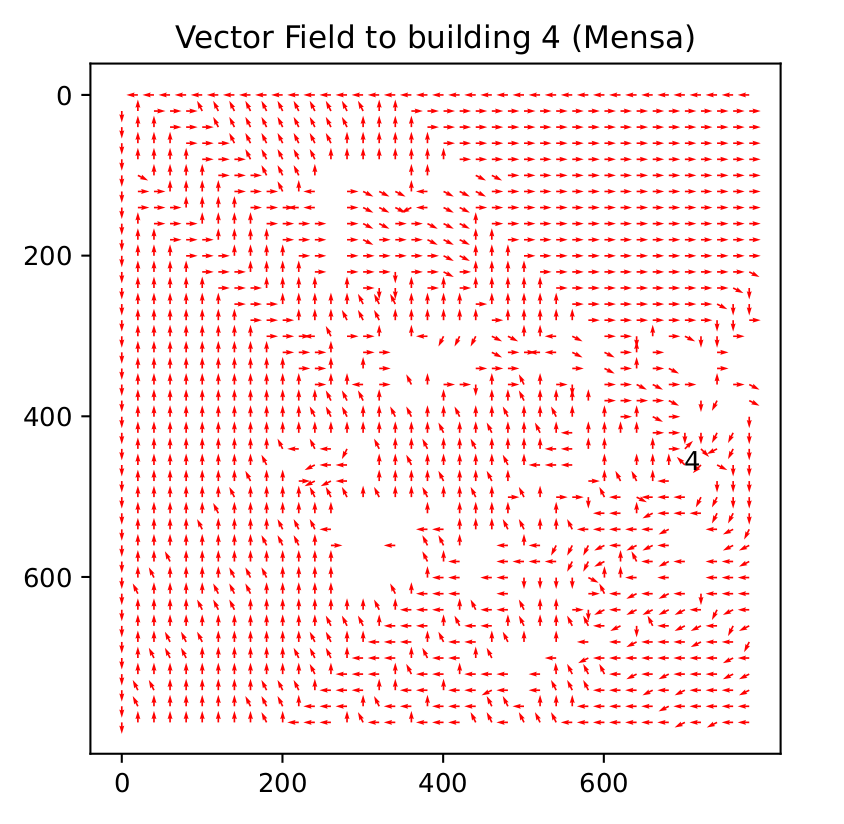
Das Flow Field repräsentiert die optimale Pfadrichtung in jeder Zelle des Grids zu einem gegebenen Ziel. Da pro Ziel wird eine $2 \text{D}$-Matrix erstellt wird, speichern wir das Ergebnis in einem $3 \text{D}$-Tensor mit der Form $30 \times 800 \times 800$. Aus dem Tensor kann man dann mit dem Index des Ziels und den aktuellen Koordinaten die Richtung bestimmen, die das Partikel optimal zum Ziel führt.